Contoh Situasi
Melambung dadu sebanyak 3 kali
Cari kebarangkalian mendapat nombor "5"
Cari kebarangkalian mendapat nombor "5"
- a) 3 kali
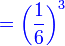
|
Penerangan
Kita tahu sudah kebarangkalian untuk mendapatkan '5' pada satu lambungan ialah
Kita tahu sudah kebarangkalian untuk mendapatkan '5' pada satu lambungan ialah  Beza soalan ini dengan soalan kebarangkalian biasa ialah
Beza soalan ini dengan soalan kebarangkalian biasa ialah lambungan di
Beza soalan ini dengan soalan kebarangkalian biasa ialah lambungan diulang untuk beberapa kali
Setiap kali lambungan dilakukan, kebarangkalian mendapatkan '5' pada lambungan tersebut
Setiap kali lambungan dilakukan, kebarangkalian mendapatkan '5' pada lambungan tersebut adalah
Beza soalan ini dengan soalan kebarangkalian biasa ialah
Beza soalan ini dengan soalan kebarangkalian biasa ialah lambungan di
Beza soalan ini dengan soalan kebarangkalian biasa ialah lambungan diulang untuk beberapa kali
Setiap kali lambungan dilakukan, kebarangkalian mendapatkan '5' pada lambungan tersebut
Setiap kali lambungan dilakukan, kebarangkalian mendapatkan '5' pada lambungan tersebut adalah  Di sini, ada tiga lambungan, dan diminta kira kebarangkalian dapat 3 kali, bermaksud
Di sini, ada tiga lambungan, dan diminta kira kebarangkalian dapat 3 kali, bermaksud setiap kali pun dapat 5
Ini bermaksud ada tiga
Di sini, ada tiga lambungan, dan diminta kira kebarangkalian dapat 3 kali, bermaksud
Di sini, ada tiga lambungan, dan diminta kira kebarangkalian dapat 3 kali, bermaksud setiap kali pun dapat 5
Ini bermaksud ada tiga  yang perlu di
Ini bermaksud ada tiga yang perlu di
Ini bermaksud ada tiga  yang perlu didarab
Lebih senang guna kuasa yang perlu didarab
Lebih senang guna kuasa
|
- b) 0 kali
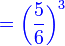
|
Penerangan
Tiada kali berjaya, bermaksud setiap kali pun
Tiada kali berjaya, bermaksud setiap kali pun tidak berjaya, iaitu
Tiada kali berjaya, bermaksud setiap kali pun tidak berjaya, iaitu tiga kali tidak berjaya
Setiap kali lambungan dilakukan, kebarangkalian TIDAK mendapatkan '5' pada lambungan tersebut adalah
Setiap kali lambungan dilakukan, kebarangkalian TIDAK mendapatkan '5' pada lambungan tersebut adalah  Perhatikan kebarangkalian tidak berjaya boleh juga dikira dari
Perhatikan kebarangkalian tidak berjaya boleh juga dikira dari 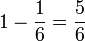 Kita perlukan
Kita perlukan ketiga-tiga kali pun tidak berjaya, maka
Kita perlukan
Kita perlukan ketiga-tiga kali pun tidak berjaya, maka
|
- c) 1 kali
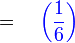
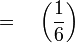
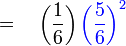
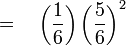
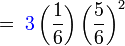
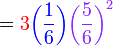
|
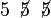
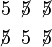
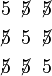
|
Penerangan
Bilangan lambungan masih lagi
Bilangan lambungan masih lagi tiga
Jika hanya 1 kali berjaya, bermakna
Jika hanya 1 kali berjaya, bermakna 2 kali tidak berjaya
Kebarangkalian 1 kali berjaya
Manakala, kebarangkalian 2 kali tidak berjaya
Kedua-dua ini perlu
Kedua-dua ini perlu didarab, jadi boleh biarkan tulis begini sebab ada sudah kurungan
Tetapi situasi manakah yang kita akan dapat berjaya 1 kali?
Mungkin berjaya kali pertama tapi gagal
Mungkin berjaya kali pertama tapi gagal di dua yang seterusnya
Mungkin juga
Mungkin juga gagal dulu baru berjaya kemudian gagal
Atau berjaya pada kali ketiga
Perhatikan untuk ketiga-tiga kes,
Perhatikan untuk ketiga-tiga kes,  perlu didarab
Perhatikan untuk ketiga-tiga kes, perlu didarab
Perhatikan untuk ketiga-tiga kes,  perlu didarab 1 kali,
Perhatikan untuk ketiga-tiga kes, perlu didarab 1 kali,
Perhatikan untuk ketiga-tiga kes,  perlu didarab 1 kali, perlu didarab 1 kali,  perlu
Perhatikan untuk ketiga-tiga kes, perlu
Perhatikan untuk ketiga-tiga kes,  perlu didarab 1 kali, perlu didarab 1 kali,  perlu didarab 2 kali
Iaitu ketiga-tiga kes pun akhirnya akan dapat perlu didarab 2 kali
Iaitu ketiga-tiga kes pun akhirnya akan dapat 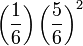 walaupun susunannya berlainan
Oleh itu, untuk menyenangkan pengiraan, terus kita darab dengan
Oleh itu, untuk menyenangkan pengiraan, terus kita darab dengan tiga
Perhatikan ada tiga bahagian walaupun susunannya berlainan
Oleh itu, untuk menyenangkan pengiraan, terus kita darab dengan
Oleh itu, untuk menyenangkan pengiraan, terus kita darab dengan tiga
Perhatikan ada tiga bahagian
 mewakili mewakili
 mewakili bilangan kes mewakili bilangan kes
 mewakili mewakili
 mewakili kebarangkalian yang berjaya mewakili kebarangkalian yang berjaya
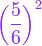 mewakili mewakili
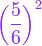 mewakili kebarangkalian yang tidak berjaya mewakili kebarangkalian yang tidak berjaya
| |
Formula Taburan Binomial
Untuk situasi
Simbol yang biasanya digunakan
- peristiwa diulang beberapa kali
- setiap kali, kebarangkalian "berjaya" adalah tetap
- Perhatikan soalan TIDAK akan menyebut perkataan binomial, kita yang perlu pastikan soalan memenuhi kriteria di atas sebelum mengunakan formula di bawah
Simbol yang biasanya digunakan
- bilangan kali diulang →
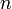
- kebarangkalian berjaya untuk setiap ulangan →
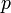
- kebarangkalian tidak berjaya untuk setiap ulangan →
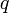 atau terus
atau terus 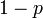
-
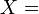 bilangan kali berjaya daripada
bilangan kali berjaya daripada 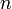 kali ulangan/percubaan
kali ulangan/percubaan
Penerangan
Pertama sekali, kita perlukan satu cara ringkas untuk mewakili kebarangkalian berjaya  kali
Kita guna kali
Kita guna 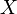 (besar) untuk mewakili bilangan berjaya,
Kita guna (besar) untuk mewakili bilangan berjaya,
Kita guna 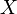 (besar) untuk mewakili bilangan berjaya, jadi jika kita mahukan ianya sama dengan (besar) untuk mewakili bilangan berjaya, jadi jika kita mahukan ianya sama dengan  Bahagian pertama ialah
Bahagian pertama ialah bilangan kes
Bahagian pertama ialah bilangan kes dan akan diberi oleh
Bahagian kedua ialah
Bahagian kedua ialah berjaya
Bahagian kedua ialah berjaya
Bahagian pertama ialah
Bahagian pertama ialah bilangan kes
Bahagian pertama ialah bilangan kes dan akan diberi oleh
Bahagian kedua ialah
Bahagian kedua ialah berjaya
Bahagian kedua ialah berjaya  kali
Bahagian ketiga ialah
Bahagian ketiga ialah tidak berjaya
Bahagian ketiga ialah tidak berjaya kali
Bahagian ketiga ialah
Bahagian ketiga ialah tidak berjaya
Bahagian ketiga ialah tidak berjaya 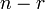 kali kali
|
Kebarangkalian berjaya  kali daripada kali daripada 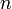 kali ulangan/percubaan
Kebarangkalian berjaya kali ulangan/percubaan
Kebarangkalian berjaya  kali daripada kali daripada 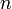 kali ulangan/percubaan kali ulangan/percubaan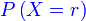 Kebarangkalian berjaya
Kebarangkalian berjaya  kali daripada kali daripada 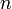 kali ulangan/percubaan kali ulangan/percubaan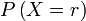 Kebarangkalian berjaya
Kebarangkalian berjaya  kali daripada kali daripada 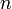 kali ulangan/percubaan kali ulangan/percubaan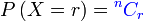 Kebarangkalian berjaya
Kebarangkalian berjaya  kali daripada kali daripada 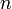 kali ulangan/percubaan kali ulangan/percubaan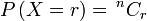 Kebarangkalian berjaya
Kebarangkalian berjaya  kali daripada kali daripada 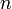 kali ulangan/percubaan kali ulangan/percubaan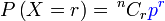 Kebarangkalian berjaya
Kebarangkalian berjaya  kali daripada kali daripada 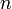 kali ulangan/percubaan kali ulangan/percubaan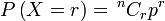 Kebarangkalian berjaya
Kebarangkalian berjaya  kali daripada kali daripada 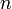 kali ulangan/percubaan kali ulangan/percubaan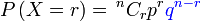
|
Contoh 1
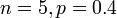
Cari kebarangkalian berjaya
- a) 2 kali
|
Penerangan
Sebenarnya, walaupun sudah ada formula, lebih senang kita buat dari pemahaman.
Tulis dahulu apa yang dikehendaki soalan
Kemudian bahagian pertama
Berjaya
Berjaya 2 kali, setiap kali kebarangkaliannya
Berjaya 2 kali, setiap kali kebarangkaliannya 0.4
Berapa kalikah tidak berjaya?
Berjaya 2 kali daripada 5 kali, jadi tidak berjaya
Berjaya 2 kali daripada 5 kali, jadi tidak berjaya 3 kali (iaitu 5-2)
Jadi tidak berjaya 3 kali, setiap kali kebarangkaliannya
Jadi tidak berjaya 3 kali, setiap kali kebarangkaliannya 0.6
Jadi tidak berjaya 3 kali, setiap kali kebarangkaliannya 0.6 Ini kerana 1-0.4 =0.6 Kira dengan kalkulator Perhatikan bergantung kepada jenis kalkulator, biasanya tanda 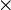 perlu ditekan selepas perlu ditekan selepas 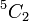 Juga, cuba jangan tulis sebagai
Semakin banyak kita menulis, semakin senang buat kesilapan / tekan salah di kalkulator
Kita boleh buat beberapa langkah berjaga-jaga untuk memastikan kita tidak tersilap jika terus menulis
Jumlah berjaya dengan tidak berjaya perlulah sama dengan bilangan ulangan
Jumlah kebarangkalian berjaya dengan tidak berjaya perlulah sama dengan 1
Juga, cuba jangan tulis sebagai
Semakin banyak kita menulis, semakin senang buat kesilapan / tekan salah di kalkulator
Kita boleh buat beberapa langkah berjaga-jaga untuk memastikan kita tidak tersilap jika terus menulis
Jumlah berjaya dengan tidak berjaya perlulah sama dengan bilangan ulangan
Jumlah kebarangkalian berjaya dengan tidak berjaya perlulah sama dengan 1
|
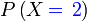
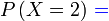
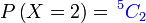
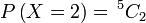
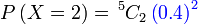
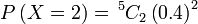
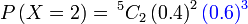
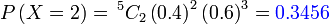
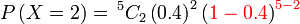
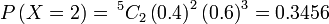
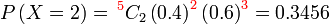
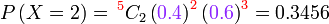
|
- Nota tambahan
- Mengapakah bilangan kes diberikan oleh
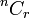 ?
? - Bukankah melibatkan susunan?
- Sebenarnya yang berlaku disini berbeza dengan sebelum ini, di mana kita telah menyusun objek berlainan
- Di sini, setiap kejayaan/kegagalan tidak dianggap unik
- Kebetulan, formula bilangan susunan adalah
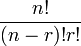 iaitu sama juga dengan
iaitu sama juga dengan 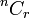
- Tetapi, boleh juga kita guna permahaman begini
- Ada
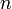 percubaan
percubaan - Kita perlukan
 percubaan berjaya, jadi kita memilih
percubaan berjaya, jadi kita memilih  tempat daripada
tempat daripada 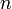 tempat untuk berjaya.
tempat untuk berjaya. - Bilangan memilih sememangnya
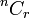
- Juga, selepas memilih tempat berjaya, secara otomatik tempat lain adalah yang tidak berjaya, jadi tidak perlu darab apa-apa lagi
- Ada
- Mengapakah bilangan kes diberikan oleh
- b) 1 kali
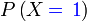
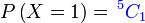
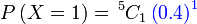
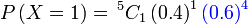
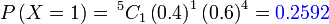
|
- c) 4 kali
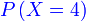
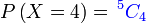
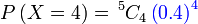
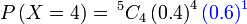
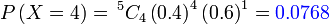
|
- d) tiada kali
Penerangan
Tiada kali sini bermaksud
Boleh guna formula
Perhatikan 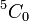 adalah sama dengan
Perhatikan adalah sama dengan
Perhatikan 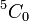 adalah sama dengan 1
Dan adalah sama dengan 1
Dan 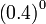 adalah sama dengan
Dan adalah sama dengan
Dan 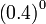 adalah sama dengan 1
Jadi tinggal adalah sama dengan 1
Jadi tinggal 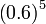 Sebenarnya situasi begini tidak memerlukan formula penuh, dan lebih baik kita terus gunakan pemahaman
Tiada kali berjaya, bermaksud
Tiada kali berjaya, bermaksud kelima-lima kali pun gagal
Sebenarnya situasi begini tidak memerlukan formula penuh, dan lebih baik kita terus gunakan pemahaman
Tiada kali berjaya, bermaksud
Tiada kali berjaya, bermaksud kelima-lima kali pun gagal
|
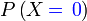
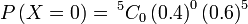 tapi lebih baik
tapi lebih baik
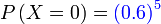
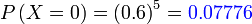
|
- e) setiap kali
Penerangan
Setiap kali di sini bermaksud
Boleh guna formula
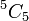 adalah sama dengan 1 adalah sama dengan 1
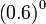 adalah sama dengan 1
Setiap kali berjaya adalah sama dengan 1
Setiap kali berjaya
|
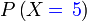
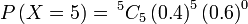 tapi lebih baik
tapi lebih baik
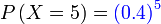
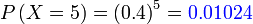
|
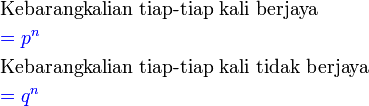
Contoh 2
Di suatu sekolah, 2 daripada 5 orang adalah perempuan
Nota tambahan
atau
| a) 10 orang dipilih secara rawak. Cari kebarangkalian 3 daripadanya adalah perempuan a) 10 orang dipilih secara rawak. Cari kebarangkalian 3 daripadanya adalah perempuan a) 10 orang dipilih secara rawak. Cari kebarangkalian 3 daripadanya adalah perempuan a) 10 orang dipilih secara rawak. Cari kebarangkalian 3 daripadanya adalah perempuan a) 10 orang dipilih secara rawak. Cari kebarangkalian 3 daripadanya adalah perempuan a) 10 orang dipilih secara rawak. Cari kebarangkalian 3 daripadanya adalah perempuan |
Penerangan
Perhatikan maklumat 2 daripada 5 orang adalah perempuan perlu difahamkan betul-betul
Adakah bermaksud ada 2 perempuan? Ada 5 orang?
TIDAK. Ini adalah suatu cara untuk menyatakan
TIDAK. Ini adalah suatu cara untuk menyatakan NISBAH perempuan kepada keseluruhan
Iaitu, maklumat sebenarnya ialah
Iaitu, maklumat sebenarnya ialah  Iaitu, maklumat sebenarnya ialah
Iaitu, maklumat sebenarnya ialah  dan BUKAN 2 dan 5 berasingan
Selain itu, mengapakah soalan in merupakan soalan taburan binomial?
Kita memilih beberapa orang. Setiap kali kita memilih satu orang,
Kita memilih beberapa orang. Setiap kali kita memilih satu orang, kebarangkalian mendapat perempuan akan ditentukan nisbah tadi, iaitu dan BUKAN 2 dan 5 berasingan
Selain itu, mengapakah soalan in merupakan soalan taburan binomial?
Kita memilih beberapa orang. Setiap kali kita memilih satu orang,
Kita memilih beberapa orang. Setiap kali kita memilih satu orang, kebarangkalian mendapat perempuan akan ditentukan nisbah tadi, iaitu  Kita memilih beberapa orang. Setiap kali kita memilih satu orang, kebarangkalian mendapat perempuan akan ditentukan nisbah tadi, iaitu
Kita memilih beberapa orang. Setiap kali kita memilih satu orang, kebarangkalian mendapat perempuan akan ditentukan nisbah tadi, iaitu  , jadi adalah tetap
Paling baik buat catatan dahulu semua maklumat
Sebenarnya dalam setiap soalan, kita perlu mendefinisikan , jadi adalah tetap
Paling baik buat catatan dahulu semua maklumat
Sebenarnya dalam setiap soalan, kita perlu mendefinisikan 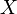 sebelum kita boleh guna tatatanda sebelum kita boleh guna tatatanda 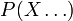 Soalan ini memerlukan bilangan
Soalan ini memerlukan bilangan perempuan dari
Soalan ini memerlukan bilangan perempuan dari 10 orang
Soalan ini meminta bilangan perempuan
Soalan ini meminta bilangan perempuan 3
Baru kira
Soalan ini memerlukan bilangan
Soalan ini memerlukan bilangan perempuan dari
Soalan ini memerlukan bilangan perempuan dari 10 orang
Soalan ini meminta bilangan perempuan
Soalan ini meminta bilangan perempuan 3
Baru kira
|
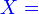
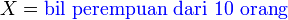
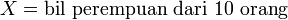 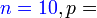
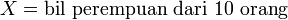 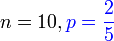
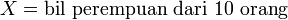 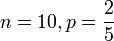 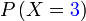
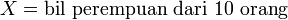 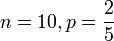 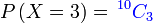
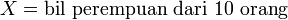 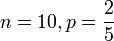 
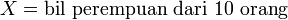 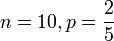 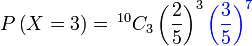
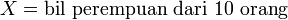 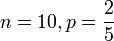 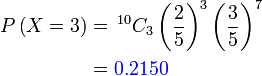
|
Nota tambahan
- Bukankah bila kita memilih beberapa objek tanpa mengantikan, pilihan pertama akan mengubah kebarangkalian seterusnya?
- Sebenarnya YA, dan kebarangkalian adalah tidak tetap, jadi sebenarnya salah untuk menggunakan formula binomial di sini
- TETAPI soalan begini mengggangap bilangan pelajar di sekolah adalah sangat besar, contohnya 2000, berbanding bilangan yang dipilih (10), jadi kebarangkalian setiap kali boleh dianggap tetap
| b) 8 orang dipilih secara rawak. Cari kebarangkalian kesemuanya adalah lelaki b) 8 orang dipilih secara rawak. Cari kebarangkalian kesemuanya adalah lelaki b) 8 orang dipilih secara rawak. Cari kebarangkalian kesemuanya adalah lelaki b) 8 orang dipilih secara rawak. Cari kebarangkalian kesemuanya adalah lelaki b) 8 orang dipilih secara rawak. Cari kebarangkalian kesemuanya adalah lelaki b) 8 orang dipilih secara rawak. Cari kebarangkalian kesemuanya adalah lelaki |
Penerangan
Perhatikan yang diminta sekarang adalah
Perhatikan yang diminta sekarang adalah lelaki, sedangkan kebarangkalian  adalah untuk perempuan
Kita boleh buat dengan
Jadi adalah untuk perempuan
Kita boleh buat dengan
Jadi
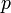 merujuk kebarangkalian merujuk kebarangkalian
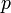 merujuk kebarangkalian mendapat lelaki, iaitu
Soalan minta
Jadi merujuk kebarangkalian mendapat lelaki, iaitu
Soalan minta
Jadi
|
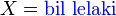
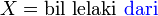
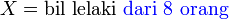
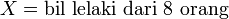
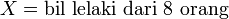 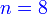
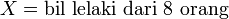 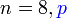
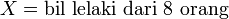 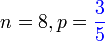
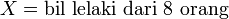 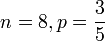
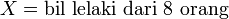 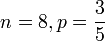 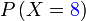
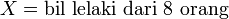 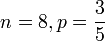 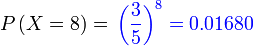
|
| b) 8 orang dipilih secara rawak. Cari kebarangkalian kesemuanya adalah lelaki b) 8 orang dipilih secara rawak. Cari kebarangkalian kesemuanya adalah lelaki b) 8 orang dipilih secara rawak. Cari kebarangkalian kesemuanya adalah lelaki |
| Kita boleh buat dengan Kita boleh buat dengan kekalkan X sebagai bilangan perempuan Jadi p masih sama Soalan minta Bermaksud bilangan perempuan ialah Bermaksud bilangan perempuan ialah sifar Tapi jawapan tetap sama |
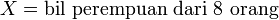
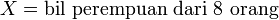 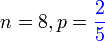
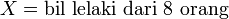 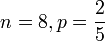 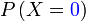
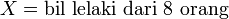 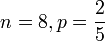 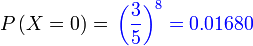
|

Julat
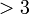
- Lebih besar daripada
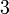
- Lebih besar daripada
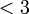
- Lebih kecil/kurang daripada
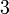
- Lebih kecil/kurang daripada
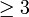
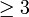 → lebih besar atau sama dengan 3 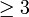 → lebih besar atau sama dengan 3 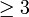 → lebih besar atau sama dengan 3 → paling kecil pun 3 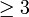 → lebih besar atau sama dengan 3 → paling kecil pun 3 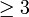 → lebih besar atau sama dengan 3 → paling kecil pun 3 → sekurang-kurangnya 3 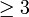 → lebih besar atau sama dengan 3 → paling kecil pun 3 → sekurang-kurangnya 3 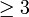 → lebih besar atau sama dengan 3 → paling kecil pun 3 → sekurang-kurangnya 3 → minimum 3 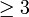 → lebih besar atau sama dengan 3 → paling kecil pun 3 → sekurang-kurangnya 3 → minimum 3 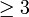 → lebih besar atau sama dengan 3 → paling kecil pun 3 → sekurang-kurangnya 3 → minimum 3 → tidak kurang dari 3 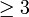 → lebih besar atau sama dengan 3 → paling kecil pun 3 → sekurang-kurangnya 3 → minimum 3 → tidak kurang dari 3 |
Penerangan
Maksud sebenar adalah
Tetapi ada banyak lagi cara untuk menyatakan julat ini dan amat penting untuk tidak tersilap mentafsir pernyataan
Kita perlu faham dulu bahawa nilai-nilai yang boleh diambil di sini ialah
Kita perlu faham dulu bahawa nilai-nilai yang boleh diambil di sini ialah 3,
Kita perlu faham dulu bahawa nilai-nilai yang boleh diambil di sini ialah 3,4,
Kita perlu faham dulu bahawa nilai-nilai yang boleh diambil di sini ialah 3,4,5 dan sebagainya
Ini bermaksud, nilai 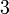 adalah nilai
Ini bermaksud, nilai adalah nilai
Ini bermaksud, nilai 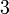 adalah nilai terkecil yang boleh diambil
Perkataan yang lebih formal ialah
Perkataan yang lebih formal ialah sekurang-kurangnya 3
Perhatikan sekurang-kurangnya 3 BUKAN bermaksud kurang,
Perhatikan sekurang-kurangnya 3 BUKAN bermaksud kurang, tetapi
boleh difahami
Perhatikan sekurang-kurangnya 3 BUKAN bermaksud kurang, tetapi
boleh difahami sebagai "paling kurang pun 3"
Perhatikan sekurang-kurangnya 3 BUKAN bermaksud kurang, tetapi
boleh difahami sebagai "paling kurang pun 3" atau "paling sikit/kecil pun 3"
Perkataan matematik pula ialah
Perhatikan minimum bermaksud nilai
Perhatikan minimum bermaksud nilai paling kecil, jadi nilai yang kita boleh ambil ialah lebih
Perhatikan minimum bermaksud nilai paling kecil, jadi nilai yang kita boleh ambil ialah lebih besar atau sama dengan nilai minimum,
Perhatikan minimum bermaksud nilai paling kecil, jadi nilai yang kita boleh ambil ialah lebih besar atau sama dengan nilai minimum, BUKAN lebih kecil
Apakah nilai-nilai yang kita TIDAK boleh ambil?
Apakah nilai-nilai yang kita TIDAK boleh ambil? 2,
Apakah nilai-nilai yang kita TIDAK boleh ambil? 2,1,
Apakah nilai-nilai yang kita TIDAK boleh ambil? 2,1,0 dan sebagainya, iaitu nilai-nilai yang lebih
Apakah nilai-nilai yang kita TIDAK boleh ambil? 2,1,0 dan sebagainya, iaitu nilai-nilai yang lebih kecil daripada 3
Ini bermakna adalah nilai terkecil yang boleh diambil
Perkataan yang lebih formal ialah
Perkataan yang lebih formal ialah sekurang-kurangnya 3
Perhatikan sekurang-kurangnya 3 BUKAN bermaksud kurang,
Perhatikan sekurang-kurangnya 3 BUKAN bermaksud kurang, tetapi
boleh difahami
Perhatikan sekurang-kurangnya 3 BUKAN bermaksud kurang, tetapi
boleh difahami sebagai "paling kurang pun 3"
Perhatikan sekurang-kurangnya 3 BUKAN bermaksud kurang, tetapi
boleh difahami sebagai "paling kurang pun 3" atau "paling sikit/kecil pun 3"
Perkataan matematik pula ialah
Perhatikan minimum bermaksud nilai
Perhatikan minimum bermaksud nilai paling kecil, jadi nilai yang kita boleh ambil ialah lebih
Perhatikan minimum bermaksud nilai paling kecil, jadi nilai yang kita boleh ambil ialah lebih besar atau sama dengan nilai minimum,
Perhatikan minimum bermaksud nilai paling kecil, jadi nilai yang kita boleh ambil ialah lebih besar atau sama dengan nilai minimum, BUKAN lebih kecil
Apakah nilai-nilai yang kita TIDAK boleh ambil?
Apakah nilai-nilai yang kita TIDAK boleh ambil? 2,
Apakah nilai-nilai yang kita TIDAK boleh ambil? 2,1,
Apakah nilai-nilai yang kita TIDAK boleh ambil? 2,1,0 dan sebagainya, iaitu nilai-nilai yang lebih
Apakah nilai-nilai yang kita TIDAK boleh ambil? 2,1,0 dan sebagainya, iaitu nilai-nilai yang lebih kecil daripada 3
Ini bermakna 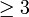 juga boleh dilihat sebagai
Perhatikan semua ini perlu difaham dengan baik kerana soalan mungkin mengunakan mana-mana bentuk. juga boleh dilihat sebagai
Perhatikan semua ini perlu difaham dengan baik kerana soalan mungkin mengunakan mana-mana bentuk.
|
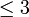
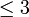 → lebih kecil atau sama dengan 3 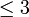 → lebih kecil atau sama dengan 3 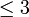 → lebih kecil atau sama dengan 3 → paling besar pun 3 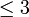 → lebih kecil atau sama dengan 3 → paling besar pun 3 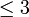 → lebih kecil atau sama dengan 3 → paling besar pun 3 → selebih-lebihnya 3 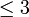 → lebih kecil atau sama dengan 3 → paling besar pun 3 → selebih-lebihnya 3 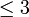 → lebih kecil atau sama dengan 3 → paling besar pun 3 → selebih-lebihnya 3 → maksimum 3 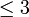 → lebih kecil atau sama dengan 3 → paling besar pun 3 → selebih-lebihnya 3 → maksimum 3 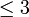 → lebih kecil atau sama dengan 3 → paling besar pun 3 → selebih-lebihnya 3 → maksimum 3 → tidak lebih dari 3 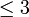 → lebih besar atau sama dengan 3 → paling kecil pun 3 → selebih-lebihnya 3 → maksimum 3 → tidak lebih dari 3 |
Penerangan
Maksud sebenar adalah
Tetapi ada banyak lagi cara untuk menyatakan julat ini dan amat penting untuk tidak tersilap mentafsir pernyataan
Kita perlu faham dulu bahawa nilai-nilai yang boleh diambil di sini ialah
Kita perlu faham dulu bahawa nilai-nilai yang boleh diambil di sini ialah 3,
Kita perlu faham dulu bahawa nilai-nilai yang boleh diambil di sini ialah 3,2,
Kita perlu faham dulu bahawa nilai-nilai yang boleh diambil di sini ialah 3,2,1 dan sebagainya
Ini bermaksud, nilai 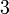 adalah nilai
Ini bermaksud, nilai adalah nilai
Ini bermaksud, nilai 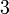 adalah nilai terbesar yang boleh diambil
Perkataan yang lebih formal ialah
Perkataan yang lebih formal ialah selebih-lebihnya 3
Perhatikan selebih-lebihnya 3 BUKAN bermaksud lebih,
Perhatikan selebih-lebihnya 3 BUKAN bermaksud lebih, tetapi
boleh difahami
Perhatikan selebih-lebihnya 3 BUKAN bermaksud lebih, tetapi
boleh difahami sebagai "paling besar/banyak pun 3"
Perkataan matematik pula ialah
Perhatikan maksimum bermaksud nilai
Perhatikan maksimum bermaksud nilai paling besar, jadi nilai yang kita boleh ambil ialah lebih
Perhatikan maksimum bermaksud nilai paling besar, jadi nilai yang kita boleh ambil ialah lebih kecil atau sama dengan nilai maksimum,
Perhatikan maksimum bermaksud nilai paling besar, jadi nilai yang kita boleh ambil ialah lebih kecil atau sama dengan nilai maksimum, BUKAN lebih besar
Apakah nilai-nilai yang kita TIDAK boleh ambil?
Apakah nilai-nilai yang kita TIDAK boleh ambil? 4,
Apakah nilai-nilai yang kita TIDAK boleh ambil? 4,5,
Apakah nilai-nilai yang kita TIDAK boleh ambil? 4,5,6 dan sebagainya, iaitu nilai-nilai yang lebih
Apakah nilai-nilai yang kita TIDAK boleh ambil? 4,5,6 dan sebagainya, iaitu nilai-nilai yang lebih besar daripada 3
Ini bermakna adalah nilai terbesar yang boleh diambil
Perkataan yang lebih formal ialah
Perkataan yang lebih formal ialah selebih-lebihnya 3
Perhatikan selebih-lebihnya 3 BUKAN bermaksud lebih,
Perhatikan selebih-lebihnya 3 BUKAN bermaksud lebih, tetapi
boleh difahami
Perhatikan selebih-lebihnya 3 BUKAN bermaksud lebih, tetapi
boleh difahami sebagai "paling besar/banyak pun 3"
Perkataan matematik pula ialah
Perhatikan maksimum bermaksud nilai
Perhatikan maksimum bermaksud nilai paling besar, jadi nilai yang kita boleh ambil ialah lebih
Perhatikan maksimum bermaksud nilai paling besar, jadi nilai yang kita boleh ambil ialah lebih kecil atau sama dengan nilai maksimum,
Perhatikan maksimum bermaksud nilai paling besar, jadi nilai yang kita boleh ambil ialah lebih kecil atau sama dengan nilai maksimum, BUKAN lebih besar
Apakah nilai-nilai yang kita TIDAK boleh ambil?
Apakah nilai-nilai yang kita TIDAK boleh ambil? 4,
Apakah nilai-nilai yang kita TIDAK boleh ambil? 4,5,
Apakah nilai-nilai yang kita TIDAK boleh ambil? 4,5,6 dan sebagainya, iaitu nilai-nilai yang lebih
Apakah nilai-nilai yang kita TIDAK boleh ambil? 4,5,6 dan sebagainya, iaitu nilai-nilai yang lebih besar daripada 3
Ini bermakna 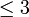 juga boleh dilihat sebagai
Perhatikan semua ini perlu difaham dengan baik kerana soalan mungkin mengunakan mana-mana bentuk. juga boleh dilihat sebagai
Perhatikan semua ini perlu difaham dengan baik kerana soalan mungkin mengunakan mana-mana bentuk.
|
Jangan terkeliru!
| Kurang daripada 3 | 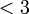
|
| Tidak kurang daripada 3 | 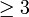
|
| Sekurang-kurangnya 3 | 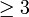
|
| Lebih daripada 3 | 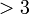
|
| Tidak lebih daripada 3 | 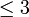
|
| Selebih-lebihnya 3 | 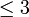
|
| Minimum 3 | 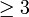
|
| Maksimum 3 | 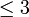
|
Pengiraan
Jika 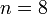 , ,Nilai-nilai 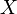 yang mungkin yang mungkin
|
→
→ 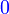 →
→ 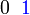 →
→ 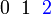 →
→ 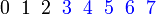 →
→ 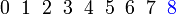
|
Penerangan
Perhatikan 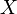 mewakili
Perhatikan mewakili
Perhatikan 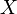 mewakili bilangan kali berjaya, jadi hanya boleh mengambil nilai
Perhatikan mewakili bilangan kali berjaya, jadi hanya boleh mengambil nilai
Perhatikan 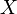 mewakili bilangan kali berjaya, jadi hanya boleh mengambil nilai nombor bulat
Tapi adakah bermula dengan mewakili bilangan kali berjaya, jadi hanya boleh mengambil nilai nombor bulat
Tapi adakah bermula dengan 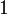 ?
Tidak. Bilangan kali berjaya boleh
Tidak. Bilangan kali berjaya boleh sifar
Paling besar ialah setiap kali berjaya ?
Tidak. Bilangan kali berjaya boleh
Tidak. Bilangan kali berjaya boleh sifar
Paling besar ialah setiap kali berjaya
|
a) 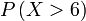
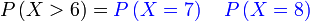
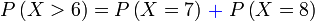
|
Penerangan
Nilai-nilai yang boleh diambil 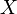 ialah
Nilai-nilai yang boleh diambil ialah
Nilai-nilai yang boleh diambil 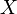 ialah 7
Nilai-nilai yang boleh diambil ialah 7
Nilai-nilai yang boleh diambil 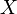 ialah 7 dan 8
Perhatikan 6
Perhatikan 6 tidak boleh diambil dalam kes ini
Jadi
Perlu
Perlu ditambah ialah 7 dan 8
Perhatikan 6
Perhatikan 6 tidak boleh diambil dalam kes ini
Jadi
Perlu
Perlu ditambah
|
b) 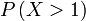
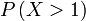 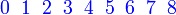
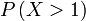 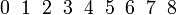
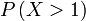 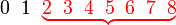
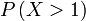 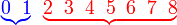
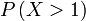 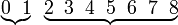
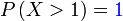 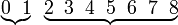
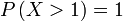 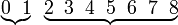
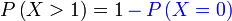 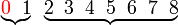
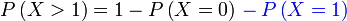 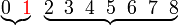
|
| Penerangan Nilai-nilai yang boleh diambil ialah Nilai-nilai yang boleh diambil ialah 2 Nilai-nilai yang boleh diambil ialah 2,3 Nilai-nilai yang boleh diambil ialah 2,3,4,5,6,7,8 Perhatikan ini bermaksud banyak pengiraan perlu dilakukan Ada cara yang lebih senang? Perhatikan kes 2,3,4,5,6,7,8 sudah Perhatikan kes 2,3,4,5,6,7,8 sudah merangkumi hampir semua kes yang mungkin Kita boleh senaraikan semua kes dahulu di bawah sebagai catatan Yang kita perlukan ialah Ini bermaksud yang TIDAK diperlukan Ini bermaksud yang TIDAK diperlukan hanya 2 kes Mengira 2 kes jauh lebih senang dari mengira 7 kes. Mengira 2 kes jauh lebih senang dari mengira 7 kes. Tapi apakah kaitan dua bahagian ini? Jumlah kebarangkalian untuk semua kes sepatutnya Jumlah kebarangkalian untuk semua kes sepatutnya 1 Jadi, kita boleh kira dengan Jadi, kita boleh kira dengan ambil 1 Jadi, kita boleh kira dengan ambil 1 tolak kes-kes yang Jadi, kita boleh kira dengan ambil 1 tolak kes-kes yang TIDAK diperlukan Kita perlu tolak Kita perlu tolak kedua-dua kes yang tidak diperlukan |
c) selebih-lebihnya 7 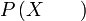 c) selebih-lebihnya 7
c) selebih-lebihnya 7 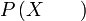 c) selebih-lebihnya 7
c) selebih-lebihnya 7 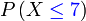 c) selebih-lebihnya 7
c) selebih-lebihnya 7 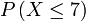 c) selebih-lebihnya 7
c) selebih-lebihnya 7 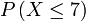 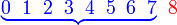 c) selebih-lebihnya 7
c) selebih-lebihnya 7 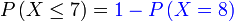 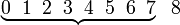
|
| Penerangan Pastikan tafsir soalan dengan betul dahulu Adakah ini melibatkan banyak kes? Ya, manakala bilangan kes yang TIDAK diperlukan Ya, manakala bilangan kes yang TIDAK diperlukan adalah sikit dan senang dikira Jadi kita guna 1 tolak |
d) tidak kurang 6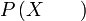 d) tidak kurang 6
d) tidak kurang 6 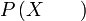 d) tidak kurang 6
d) tidak kurang 6 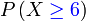 d) tidak kurang 6
d) tidak kurang 6 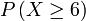 d) tidak kurang 6
d) tidak kurang 6 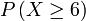 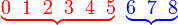 d) tidak kurang 6
d) tidak kurang 6  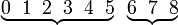
|
| Penerangan Pastikan tafsir soalan dengan betul dahulu Adakah ini melibatkan banyak kes? Bilangan kes yang diperlukan Bilangan kes yang diperlukan kurang dari yang tidak diperlukan Jadi, Jadi, TIADA sebab untuk guna 1 tolak Sebaliknya, terus sahaja |

Contoh 3
Penerangan
Pastikan tafsir semua maklumat dan soalan dahulu
Mula dengan
Tafsir soalan betul-betul
baru tentukan cara pengiraan
Memerlukan 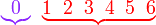 Memerlukan
Memerlukan 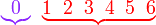 banyak kes, kes yang tidak diperlukan
Memerlukan banyak kes, kes yang tidak diperlukan
Memerlukan 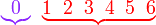 banyak kes, kes yang tidak diperlukan sedikit, jadi
Memerlukan banyak kes, kes yang tidak diperlukan sedikit, jadi
Memerlukan 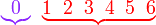 banyak kes, kes yang tidak diperlukan sedikit, jadi guna 1 tolak kes tidak diperlukan
baru kira banyak kes, kes yang tidak diperlukan sedikit, jadi guna 1 tolak kes tidak diperlukan
baru kira
|
Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata.
Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata.
Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata.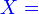 Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata.
Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata.  Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata.
Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata. 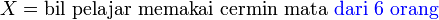 Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata.
Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata. 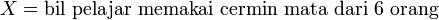  Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata.
Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata. 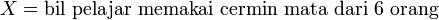 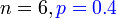 Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata.
Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata. 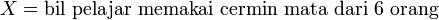 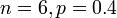 Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata.
Di suatu sekolah, 40% pelajar memakai cermin mata. 6 orang dipilih secara rawak. Cari kebarangkalian sekurang-kurangnya 1 orang memakai cermin mata. 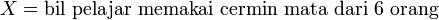 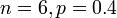 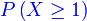
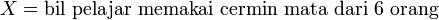 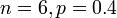 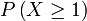
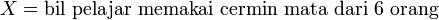 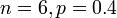 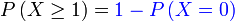
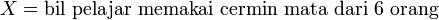 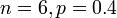 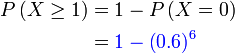
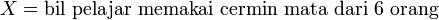 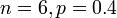 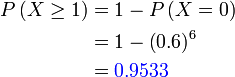
|
Min dan sisihan piawai
Berapakah anggaran kali berjaya jika
Formula
a) 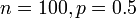 a)
a) 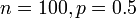 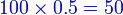
|
| Situasi ialah ada Situasi ialah ada 100 kali percubaan, setiap kali percubaan kebarangkalian berjaya Situasi ialah ada 100 kali percubaan, setiap kali percubaan kebarangkalian berjaya adalah 0.5, atau Situasi ialah ada 100 kali percubaan, setiap kali percubaan kebarangkalian berjaya adalah 0.5, atau 50%, atau Situasi ialah ada 100 kali percubaan, setiap kali percubaan kebarangkalian berjaya adalah 0.5, atau 50%, atau boleh dilihat sebagai separuh-separuh peluang untuk berjaya atau gagal. Jelas bahawa anggaran kali berjaya dari 100 kali ialah Jelas bahawa anggaran kali berjaya dari 100 kali ialah 50, Jelas bahawa anggaran kali berjaya dari 100 kali ialah 50, iaitu |
- b)
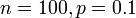
-
Formula
- Min,
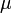
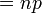
- Formula ini jelas kalau melihat contoh-contoh di atas
- Sisihan piawai,
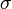
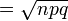
- Formula in perlu dihafal tanpa pemahaman pada masa ini
- Perhatikan varians,
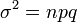
Graf taburan binomial
Penerangan
X mengambil nilai-nilai
Untuk menggambarkan semua kebarangkalian yang diambil untuk nilai-nilai
Untuk menggambarkan semua kebarangkalian yang diambil untuk nilai-nilai 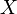 berlainan, kita boleh
Untuk menggambarkan semua kebarangkalian yang diambil untuk nilai-nilai berlainan, kita boleh
Untuk menggambarkan semua kebarangkalian yang diambil untuk nilai-nilai 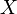 berlainan, kita boleh lukis graf berlainan, kita boleh lukis graf
|
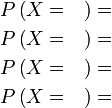
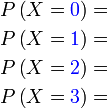
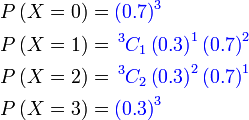
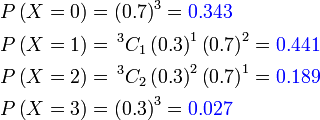
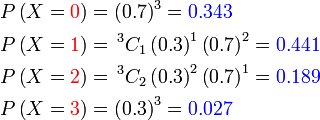
|
- → jumlah kebarangkalian
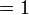
- Fakta ini boleh digunakan untuk menyelesaikan soalan-soalan di mana graf sudah dilukis tetapi ada nilai yang perlu dicari
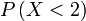
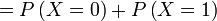
-
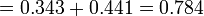
- Iaitu, jika sudah ada graf/diberi graf dalam soalan, nilai kebarangkalian terus dibaca dari graf dan tidak perlu kira dari formula lagi
-
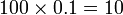
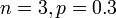
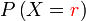 , bilangan sebenarnya lebih logik dilabel sebagai
, bilangan sebenarnya lebih logik dilabel sebagai 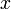
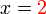 ,
, 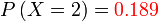
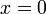 paling baik jangan diletakkan tepat di paksi mencancang kerana akan susah nampak garis
paling baik jangan diletakkan tepat di paksi mencancang kerana akan susah nampak garis.png)
.png)
.png)
a).png)
b).png)
).png)
.png)