Punca-punca persamaan kuadratik
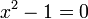
- Punca - punca :
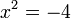
- Punca - punca :
Contoh
Diberi bahawa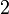 ialah satu punca untuk persamaan
ialah satu punca untuk persamaan 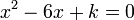 . Cari nilai
. Cari nilai 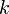 .
.
Hasil darab Sifar
- Jika
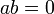
- Apakah nilai-nilai
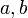 yang mungkin?
yang mungkin?

|
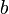
|
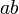
|
|---|---|---|
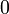
| ||
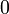
| ||
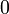
| ||
|
| ||
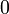
| ||
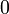
| ||
|
| ||
| Mungkinkah kedua-duanya bukan kosong? | ||

|
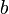
|
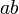
|
|
| ||
|
| ||
|
| ||
- Jadi
- Jika
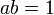 ,
,
Selesaikan
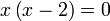
|
| Penerangan |
- Jika
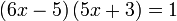
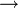
Penyelesaian Persamaan Kuadratik dengan Pemfaktoran
- Perhatikan perbezaan besar antara langkah menyelesaikan persamaan linear dengan kuadratik
| Linear | Kuadratik |
|---|---|
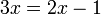 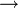
|
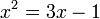 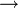
|
Selesaikan
| Penerangan |
a) 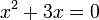
|
- Jika
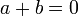 ,
,
| Penerangan |
b) 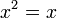
|
| Penerangan |
c) 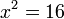
|
- Atau
| Penerangan |
c) 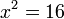
|
| Penerangan |
d) 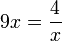
|
- Atau
| Penerangan |
d) 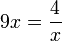
|
Pemfaktoran ax^2+bx+c=0
Bandingkan
Kembangkan
Tulis sebagai hasil darab
Kembangkan
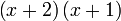
|
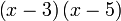
|
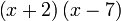
|
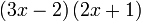
|
- Jadi dari contoh-contoh atas, kita melihat bahawa hasil pengembangan dalam bentuk
Tulis sebagai hasil darab
Selesaikan
| Penerangan |
a) 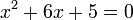
|
| Langkah tambahan |
| Penerangan |
b) 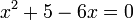
|
| Langkah tambahan |
| Penerangan |
c) 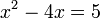
|
- d)
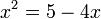
- e)
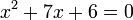
- f)
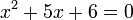
- g)
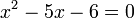
- h)
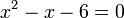
- i)
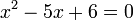
- j)
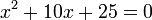
- k)

| Penerangan |
l) 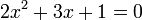
|
| Langkah tambahan |
- m)
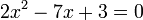
- n)
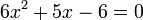
| Penerangan |
o) 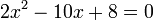
|
| Penerangan |
p) 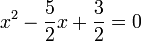
|
| Penerangan |
q) 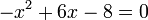
|
Sebelum pemfaktoran
- Jadi kita lihat ada beberapa kes di mana kita perlu buat sesuatu (selain pindah dan susun) sebelum kita faktorkan
Contoh
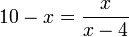
|
| Langkah-langkah |
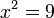
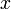 yang bila dikuasa-duakan akan menjadi
yang bila dikuasa-duakan akan menjadi 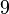 ?
?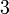
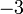
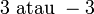
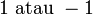

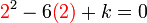
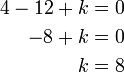
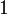
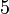
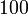
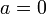 ,
, 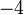
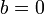 ,
, 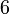
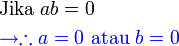

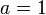 ?
? 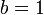 ?
?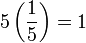
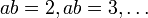 ?
?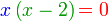
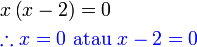
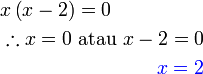
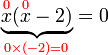
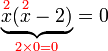
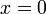
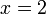
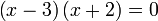
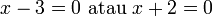
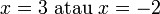
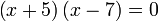
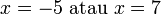
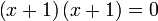
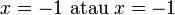
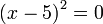
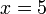
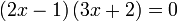
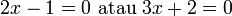
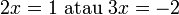

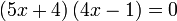
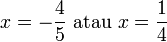
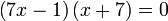

 ?
? 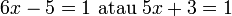 ?
?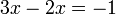
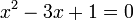

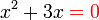
 sifar
sifar sifar?
sifar?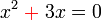 , bukannya darab
, bukannya darab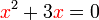
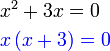
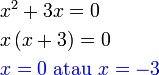
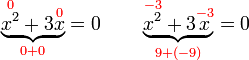
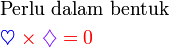
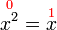
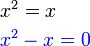
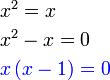
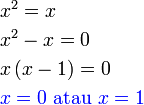
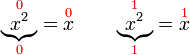

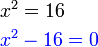
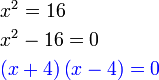
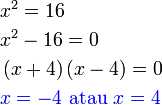
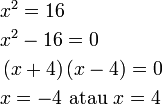
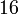 , tapi kita tahu sekarang sudah bahawa sebenarnya ada dua jawapan, satu positif dan satu negatif.
, tapi kita tahu sekarang sudah bahawa sebenarnya ada dua jawapan, satu positif dan satu negatif.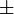
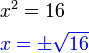
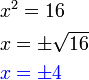
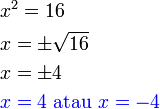
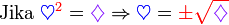
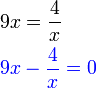
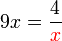
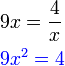
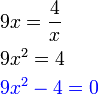
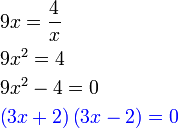
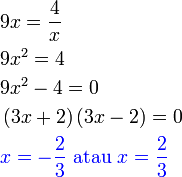
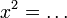
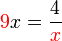
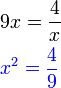
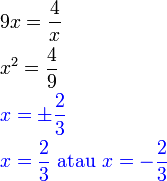

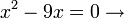
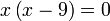
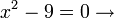
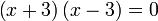
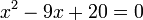
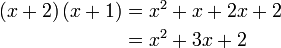
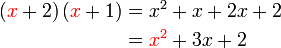
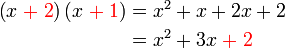
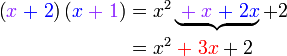
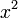 dari hasil darab sebutan
dari hasil darab sebutan 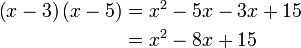
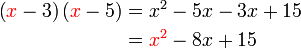
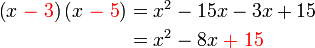
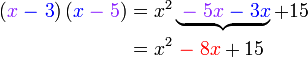
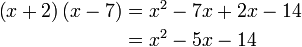
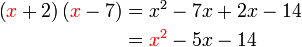
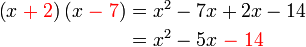
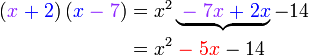
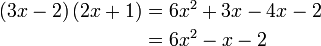
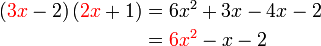
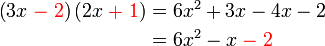
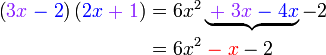
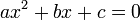 boleh kita cuba faktorkan balik ke bentuk
boleh kita cuba faktorkan balik ke bentuk 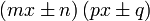

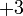
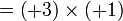
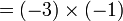

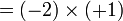
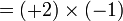
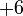
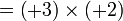
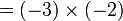
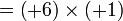
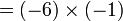
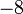
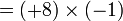
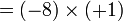
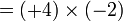
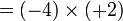

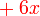
 sama dengan
sama dengan 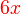 , jadi adalah betul
, jadi adalah betul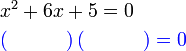
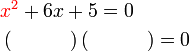
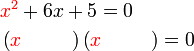
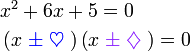
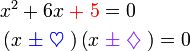
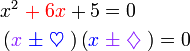
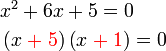
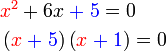
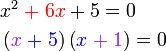
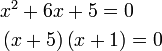
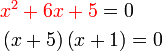
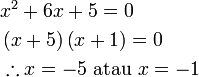
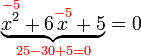
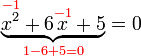
.png)
%2b5%2cred(x)%2b1%2cred(x%5e(2))).png)
%2cxred(%2b1)%2cx%5e(2)red(%2b5)).png)
%2b5%2cxred(%2b1)%2cred(%2bx)%2cx%5e(2)%2b5).png)
%2cred(%2b5x)%2cred(x)%2b1%2c%2bx%2cx%5e(2)%2b5).png)
%2cx%2b1%2cred(%2bx)%2cx%5e(2)%2b5red(%2b6x)).png)
%2b5%2b6x)).png)

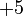 ?
?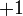 tadi, dan mendapat
tadi, dan mendapat 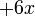 untuk sebutan
untuk sebutan 
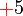 , samaada kedua-duanya positif atau kedua-duanya negatif
, samaada kedua-duanya positif atau kedua-duanya negatif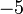 dan
dan 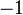
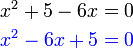
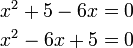
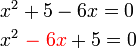
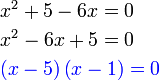
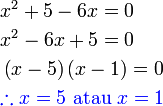
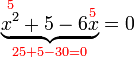
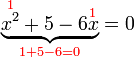
%2cred(x)).png)
%2cxred(-1)).png)
)).png)
red(%2b5)).png)
purple(-5)%2cpurple(-5x)%2cpurple(x)blue(-1)%2cblue(-x)x%5e(2)%2b5red(-6x)).png)
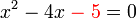
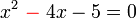
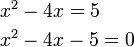
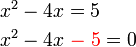
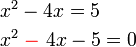
-5-4x).png)
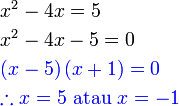
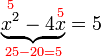
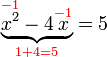
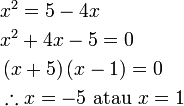
-5%2b4x).png)
 ?
?
 ?
?
%2b6%2b7x).png)
%2b6%2b5x).png)
-6-x).png)
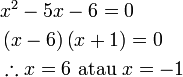
-6-5x).png)
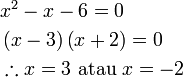
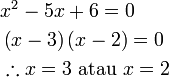
%2b6-5x).png)
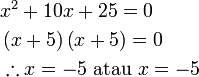
%2b25%2b10x).png)
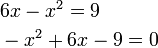
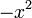 akan merumitkan keadaan jadi paling baik hapuskan tanda negatif pada
akan merumitkan keadaan jadi paling baik hapuskan tanda negatif pada 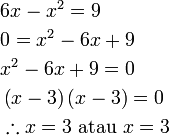
%2b9-6x).png)
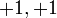 dengan
dengan 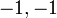
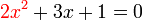
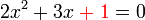
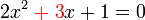
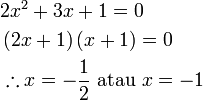
%2cred(x)%2cred(2x%5e(2))).png)
%2b1%2b3x).png)
%2b3-5x).png)
%2b3-7x).png)
-6%2b5x).png)
 tetap
tetap 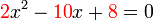
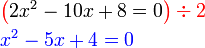
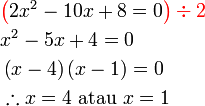
%2b4-5x).png)
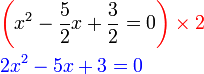
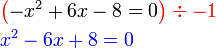
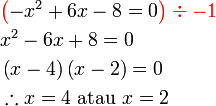
%2b8-6x).png)

%2b40-13x).png)
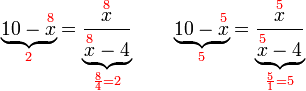
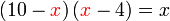
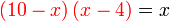
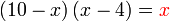
 ?
?