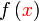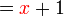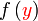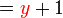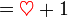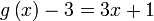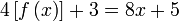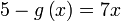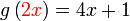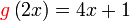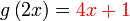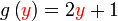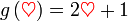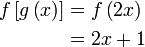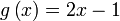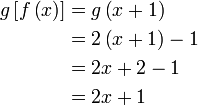Mencari Pemalar / Mencari Nilai
Diberi 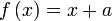 dan dan 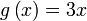 . .Cari nilai  jika jika 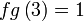 Diberi
Diberi 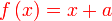 dan dan 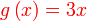 . .Cari nilai  jika jika 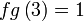 Diberi
Diberi 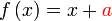 dan dan 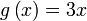 . .Cari nilai 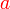 jika jika 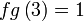 Diberi
Diberi 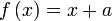 dan dan 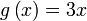 . .Cari nilai  jika jika  Diberi
Diberi 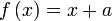 dan dan 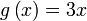 . .Cari nilai  jika jika  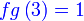 Diberi
Diberi 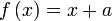 dan dan 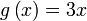 . .Cari nilai  jika jika 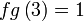
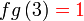 Diberi
Diberi 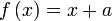 dan dan 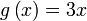 . .Cari nilai  jika jika 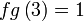
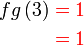 Diberi
Diberi 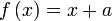 dan dan 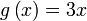 . .Cari nilai  jika jika 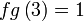
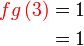 Diberi
Diberi 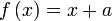 dan dan 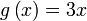 . .Cari nilai  jika jika 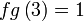
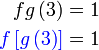 Diberi
Diberi 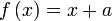 dan dan 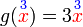 . .Cari nilai  jika jika 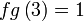
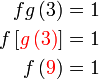 Diberi
Diberi 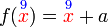 dan dan  . .Cari nilai  jika jika 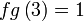
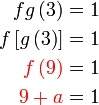 Diberi
Diberi  dan dan  . .Cari nilai  jika jika 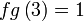
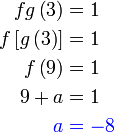 Semak :
Semak :
Semak :
Semak :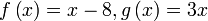 Semak :
Semak :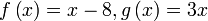 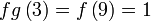
|
Penerangan
Kita diberi kedua-dua f dan g
Tetapi ada pemalar yang tidak diketahui nilainya
Dan kita juga diberi
Iaitu suatu persamaan
Kita pernah buat soalan yang mencari pemalar sebelum ini, hanya di sini melibatkan fungsi gubahan jadi mungkin lebih panjang jalan kerjanya
Jadi kita mula dari
Jadi kita mula dari persamaan yang diberi
Sebelah kanan
Sebelah kiri, 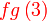 tidak begitu senang dikira terus, jadi buat langkah-demi-langkah, tapi dari atas ke bawah di sebelah kiri
Letak kurungan
Kira yang di dalam kurungan
Seterusnya
Selesaikan tidak begitu senang dikira terus, jadi buat langkah-demi-langkah, tapi dari atas ke bawah di sebelah kiri
Letak kurungan
Kira yang di dalam kurungan
Seterusnya
Selesaikan
|
Diberi 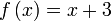 dan dan 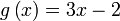 . .Cari nilai 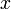 sehinggakan sehinggakan 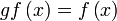 .
Diberi .
Diberi 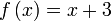 dan dan 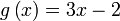 . .Cari nilai 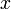 sehinggakan sehinggakan 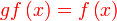 . .
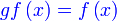
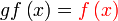
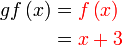
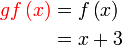
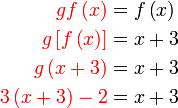
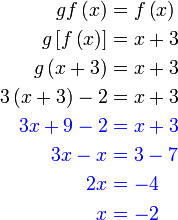
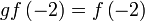 
|
Penerangan
Apakah 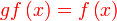 ?
Adakah ianya formula/arahan untuk gf atau suatu persamaan yang perlu dipenuhi?
Dalam kes ini adalah suatu persamaan
Kita pernah buat soalan yang mencari nilai yang memenuhi persamaan sebelum ini, tapi yang hanya melibatkan satu fungsi
Jadi, mula dengan persamaan
Sebelah kanan
Diganti
Sebelah kiri
Perlu cari formula ?
Adakah ianya formula/arahan untuk gf atau suatu persamaan yang perlu dipenuhi?
Dalam kes ini adalah suatu persamaan
Kita pernah buat soalan yang mencari nilai yang memenuhi persamaan sebelum ini, tapi yang hanya melibatkan satu fungsi
Jadi, mula dengan persamaan
Sebelah kanan
Diganti
Sebelah kiri
Perlu cari formula 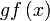 Boleh cari berasingan dahulu di tempat lain baru masukkan ke sini
Atau terus buat di sini (dari atas ke bawah di sebelah kiri) pun boleh
Selesaikan seperti biasa
Kita perlu semak bahawa
Kita perlu semak bahawa
Boleh cari berasingan dahulu di tempat lain baru masukkan ke sini
Atau terus buat di sini (dari atas ke bawah di sebelah kiri) pun boleh
Selesaikan seperti biasa
Kita perlu semak bahawa
Kita perlu semak bahawa memenuhi memenuhi 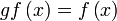 iaitu
jadi sah betul
iaitu
jadi sah betul
|
Fungsi Sama
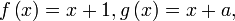
- Jika
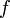 dan
dan 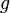 adalah fungsi sama
adalah fungsi sama 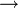 arahan adalah sama
arahan adalah sama
- arahan
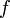 ialah objek
ialah objek 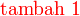
- arahan
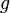 ialah objek
ialah objek 
- kedua-dua arahan ini diberi adalah sama, jadi sudah pasti
- arahan
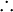
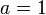
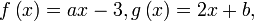
- Jika
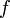 dan
dan 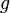 adalah fungsi sama
adalah fungsi sama - arahan
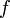 ialah
ialah  dengan objek, kemudian
dengan objek, kemudian 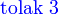
- arahan
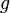 ialah
ialah  dengan objek, kemudian
dengan objek, kemudian 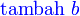
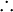
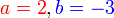
- Perhatikan

- Tapi JANGAN tulis
 , seakan-akan sedang menyelesaikan persamaan
, seakan-akan sedang menyelesaikan persamaan - Yang sebenarnya sedang dilakukan ialah MEMBANDING dua arahan ini, yang diberi adalah sama
- Mungkin tidak terselesai jika mula dengan
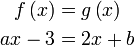
- Adakah langkah seterusnya sepatutnya
 ?
?- Sudah tentu tidak.
- Jadi paling baik jangan tulis begini, sebaliknya tulis kedua-dua fungsi berasingan dan bandingkan
- Sebenarnya kita boleh buat juga
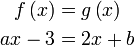
- Tetapi kita mesti sedar kita sedang membanding kiri dengan sebelah kanan
- Jadi langkah seterusnya adalah membanding (dan bukan pindah seakan-akan menyelesaikan
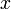 )
)
- Perhatikan
- Tetapi kita mungkin tertanya, jika
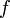 dan
dan 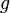 fungsi sama, kenapakah diberikan nama berlainan?
fungsi sama, kenapakah diberikan nama berlainan?
- Biasanya soalan bukan begini, tetapi kita akan lihat ada beberapa keadaan kita perlu membanding dua fungsi yang sepatutnya sama
Contoh 1
Diberi 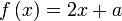 . Cari nilai . Cari nilai  jika jika 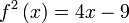 .
Diberi .
Diberi 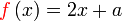 . Cari nilai . Cari nilai  jika jika 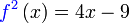 .
Diberi .
Diberi 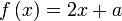 . Cari nilai . Cari nilai  jika jika 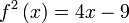 . .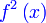 Diberi
Diberi 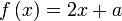 . Cari nilai . Cari nilai  jika jika 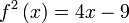 . .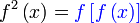 Diberi
Diberi  . Cari nilai . Cari nilai  jika jika 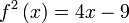 . .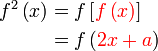 Diberi
Diberi 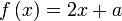 . Cari nilai . Cari nilai  jika jika 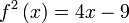 . .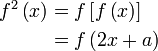 Diberi
Diberi 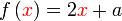 . Cari nilai . Cari nilai  jika jika 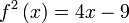 . .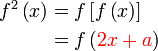 Diberi
Diberi 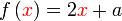 . Cari nilai . Cari nilai  jika jika 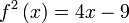 . .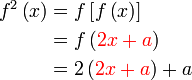 Diberi
Diberi 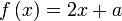 . Cari nilai . Cari nilai  jika jika 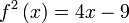 . .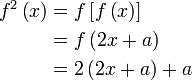 Diberi
Diberi 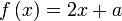 . Cari nilai . Cari nilai  jika jika 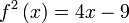 . .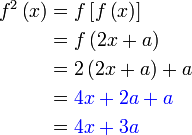 Diberi
Diberi 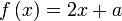 . Cari nilai . Cari nilai  jika jika 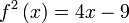 . .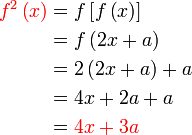 Diberi
Diberi 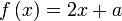 . Cari nilai . Cari nilai  jika jika 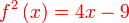 . .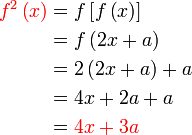 Diberi
Diberi 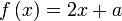 . Cari nilai . Cari nilai  jika jika 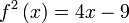 . . Diberi
Diberi 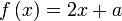 . Cari nilai . Cari nilai  jika jika 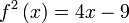 . .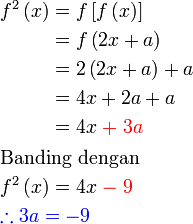 Diberi
Diberi 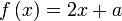 . Cari nilai . Cari nilai  jika jika 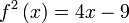 . .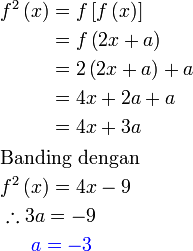 Semak :
Semak : 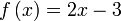 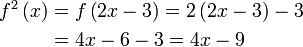
|
Penerangan
Analisis : Diberi sudah fungsi 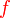 , bermaksud sebenarnya , bermaksud sebenarnya 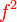 boleh dicari dari sana, kenapa formula untuk boleh dicari dari sana, kenapa formula untuk 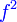 dibagi dalam soalan?
Kita cuba cari dulu dibagi dalam soalan?
Kita cuba cari dulu 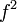 dari dari 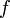 yang diberi dan tengok apa yang berlaku
Berhati-hati dengan langkah seterusnya
Ringkaskan
Sambung analisis : Kita mendapat
Tetapi soalan sudah memberikan maklumat
Jadi langkah seterusnya ialah
Jadi langkah seterusnya ialah membandingkan kedua - dua nya
Semak bahawa nilai yang kita dapat sememangnya memenuhi maklumat yang diberikan yang diberi dan tengok apa yang berlaku
Berhati-hati dengan langkah seterusnya
Ringkaskan
Sambung analisis : Kita mendapat
Tetapi soalan sudah memberikan maklumat
Jadi langkah seterusnya ialah
Jadi langkah seterusnya ialah membandingkan kedua - dua nya
Semak bahawa nilai yang kita dapat sememangnya memenuhi maklumat yang diberikan
|
Contoh 2
Diberi  dan dan 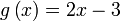 . .Cari nilai  dan dan 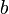 jika jika 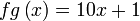 .
Diberi .
Diberi  dan dan 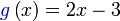 . .Cari nilai  dan dan 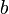 jika jika 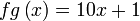 .
Diberi .
Diberi  dan dan 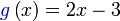 . .Cari nilai  dan dan 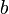 jika jika 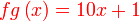 . .
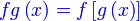
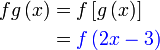
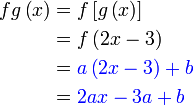
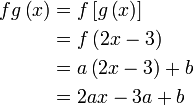

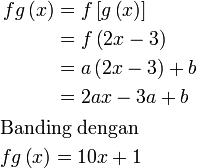


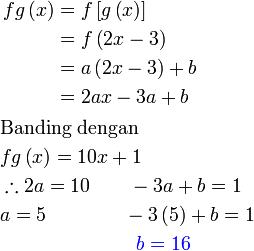
 Semak :
Semak :
Semak :
Semak : 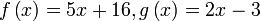 Semak :
Semak : 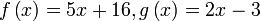 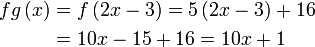
|
|
Penerangan
Analisis: Diberi 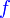 dan dan 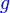 , bermaksud boleh
Analisis: , bermaksud boleh
Analisis:Diberi 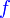 dan dan 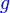 , bermaksud boleh cari , bermaksud boleh cari 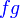 Kemudian Analisis: Diberi 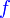 dan dan 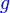 , bermaksud boleh cari , bermaksud boleh cari 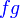 Kemudian banding dengan 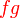 yang sudah diberi
Boleh ringkas lagi?
Boleh ringkas lagi? Tidak
Sambung analisis : yang sudah diberi
Boleh ringkas lagi?
Boleh ringkas lagi? Tidak
Sambung analisis : 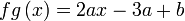 nampak agak merumitkan, tapi ingat nampak agak merumitkan, tapi ingat  dan dan 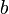 adalah pemalar, bukan objek. Jadi ungkapan seperti adalah pemalar, bukan objek. Jadi ungkapan seperti 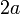 sebenarnya mewakili satu nilai tunggal
Jadi apakah arahan yang dimaksudkan oleh sebenarnya mewakili satu nilai tunggal
Jadi apakah arahan yang dimaksudkan oleh 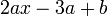 ? ?
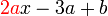
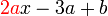 suatu nilai darab dengan objek 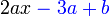
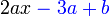 tambah/tolak suatu nilai Jadi bandingkan Pastikan banding "bahagian-bahagian" formula yang sepadan Selesaikan |
Bandingkan
- Diberi
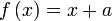 dan
dan 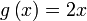 .
. - Cari nilai
 jika
jika 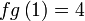
-
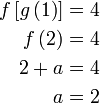
- Perhatikan
- Yang diberi,
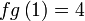 merupakan satu persamaan
merupakan satu persamaan - Kita mula dengan persamaan tersebut
- Yang diberi,
- Diberi
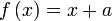 dan
dan 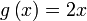 .
. - Cari nilai
 jika
jika 
-
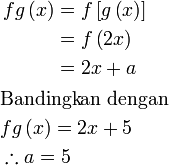
- Perhatikan
- Yang diberi,
 merupakan formula untuk fungsi gubahan
merupakan formula untuk fungsi gubahan - Kita paling baik jangan mula dengan formula tersebut, sebaliknya cari dengan maklumat kemudian bandingkan
- Yang diberi,
- Diberi
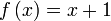 dan
dan 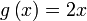 .
. - Cari nilai
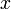 sehinggakan
sehinggakan 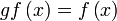
-
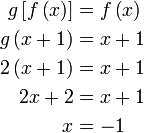
- Perhatikan
- Yang diberi,
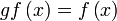 merupakan satu persamaan
merupakan satu persamaan - Kita mula dengan persamaan tersebut
- Yang dicari adalah suatu nilai objek, bukan pemalar dalam formula fungsi
- Yang diberi,
Diberi fungsi gubahan, cari fungsi
Jenis A
Contoh 1
Diberi 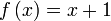 dan dan 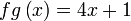 . .Cari  .
Diberi .
Diberi 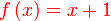 dan dan 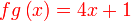 . .Cari 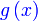 .
Diberi .
Diberi 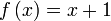 dan dan 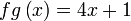 . .Cari  .
Diberi .
Diberi 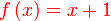 dan dan 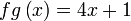 . .Cari  .
Diberi .
Diberi 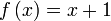 dan dan 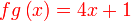 . .Cari  . .
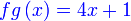
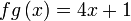
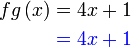

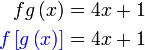
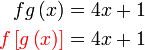 Diberi
Diberi 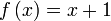 dan dan 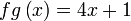 . .Cari 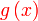 . .
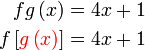 Diberi
Diberi 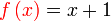 dan dan 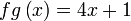 . .Cari  . .
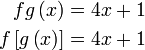 Diberi
Diberi 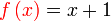 dan dan 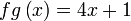 . .Cari  . .
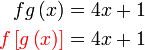 Diberi
Diberi 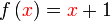 dan dan 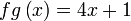 . .Cari  . .
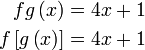 Diberi
Diberi 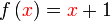 dan dan 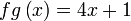 . .Cari  . .
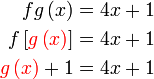
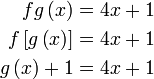

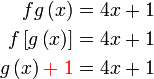
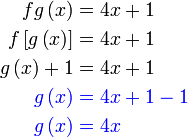 Diberi
Diberi 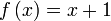 dan dan 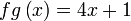 . .Cari  . .
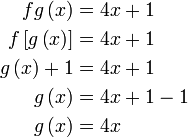 Diberi
Diberi 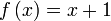 dan dan 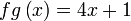 . .Cari  . .
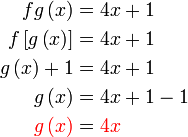 Diberi
Diberi 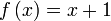 dan dan 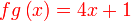 . .Cari  . .
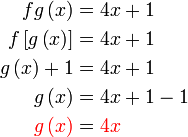 Semak :
Semak :
Semak :
Semak : 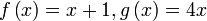 Semak :
Semak : 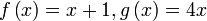 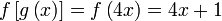
|
Penerangan
Apakah beza soalan ini dengan soalan fungsi gubahan biasa?
Sebelum ini, kita diberi 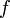 dan dan 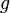 , kemudian cari , kemudian cari 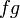 (atau (atau 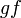 )
Sekarang, kita diberi fungsi gubahan, dan hanya salah satu fungsi tersebut, cari fungsi yang satu lagi
Mula dari mana?
Tidak apa-apa yang boleh dibuat dengan
Jadi dalam kes ini kita cuba mula dengan )
Sekarang, kita diberi fungsi gubahan, dan hanya salah satu fungsi tersebut, cari fungsi yang satu lagi
Mula dari mana?
Tidak apa-apa yang boleh dibuat dengan
Jadi dalam kes ini kita cuba mula dengan 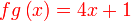
(walaupun ianya merupakan formula dan bukan persamaan) Apa yang boleh dibuat di sebelah kiri/kanan? Sebelah kanan Sebelah kanan disalin Sebelah kiri Sebelah kiri letak kurungan Untuk seterusnya, apakah yang boleh dibuat dengan 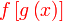 ?
Biasanya kita akan
Biasanya kita akan masukkan ?
Biasanya kita akan
Biasanya kita akan masukkan  (fungsi dalam)
Tetapi di sini kita tiada (fungsi dalam)
Tetapi di sini kita tiada 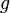 , dan sememangnya , dan sememangnya 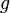 yang dicari
Kita hanya ada yang dicari
Kita hanya ada 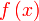 Jadi apakah yang boleh dibuat dengan
Kita ada
Jadi
Jadi apakah yang boleh dibuat dengan
Kita ada
Jadi  akan jadi
Jadi akan jadi
Jadi  akan jadi akan jadi 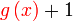
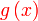 Jadi
Jadi pindah yang lain/susun semula
Bagaimanakah menyemak?
Memastikan
Jadi
Jadi pindah yang lain/susun semula
Bagaimanakah menyemak?
Memastikan 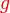 yang kita dapat sememangnya
Memastikan yang kita dapat sememangnya
Memastikan 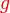 yang kita dapat sememangnya memberikan yang kita dapat sememangnya memberikan  yang diberi
Boleh tulis semula f dan g dahulu supaya senang rujuk yang diberi
Boleh tulis semula f dan g dahulu supaya senang rujuk
|
| Tulis langkah pertama sahaja | |
| Diberi | |
|---|---|
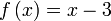
|
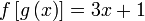
|
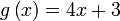
|
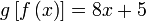
|

|
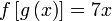
|
Contoh 2
Diberi 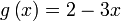 dan dan 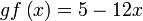 . Cari . Cari 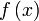
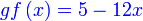
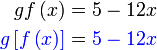
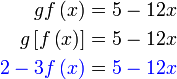
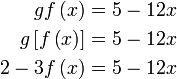 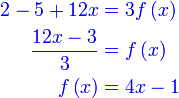 Semak :
Semak :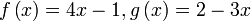 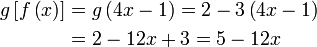
|
Cuba sendiri dahulu
Pastikan 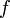 yang didapati sememangnya memberikan yang didapati sememangnya memberikan 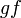 dalam soalan.
Jika tidak, semak setiap langkah sehingga dapat jawapan yang sememangya memberikan dalam soalan.
Jika tidak, semak setiap langkah sehingga dapat jawapan yang sememangya memberikan 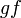 tersebut
Mula dengan formula fungsi gubahan
Letak kurungan, perhatikan fungsi dalam tidak diberi, yang diberi fungsi luar
ganti berhati-hati
yang diperlukan ialah tersebut
Mula dengan formula fungsi gubahan
Letak kurungan, perhatikan fungsi dalam tidak diberi, yang diberi fungsi luar
ganti berhati-hati
yang diperlukan ialah 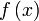 sahaja, jadikan sebagai subjek dengan cara biasa sahaja, jadikan sebagai subjek dengan cara biasa
|

Jenis B
Contoh 1
Diberi 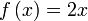 dan dan 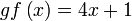 . .Cari  .
Diberi .
Diberi 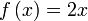 dan dan 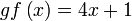 . .Cari  . .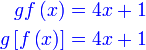 Diberi
Diberi 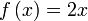 dan dan 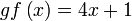 . .Cari  . .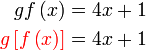 Diberi
Diberi 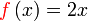 dan dan 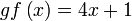 . .Cari  . .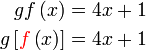 Diberi
Diberi 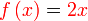 dan dan 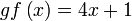 . .Cari  . .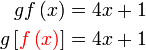 Diberi
Diberi 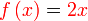 dan dan 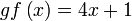 . .Cari  . .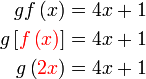 Diberi
Diberi 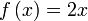 dan dan 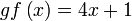 . .Cari  . .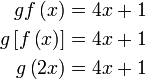
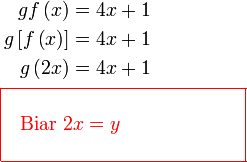
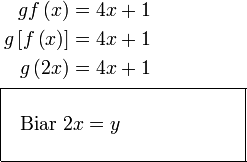
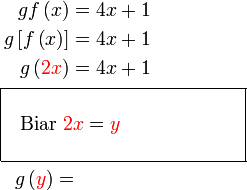
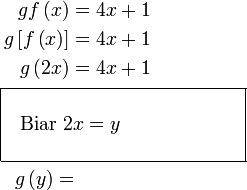
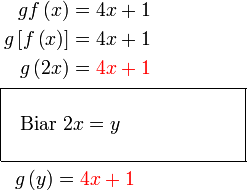
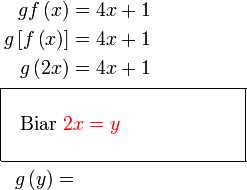
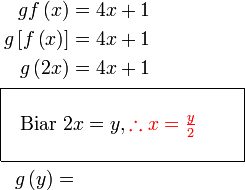
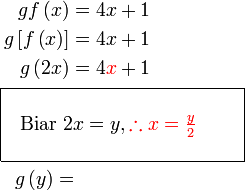
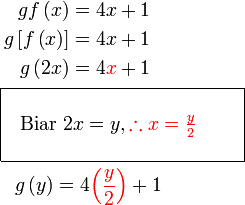
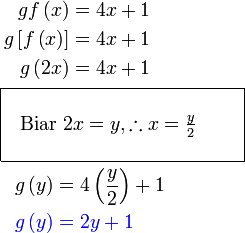
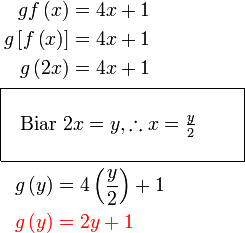
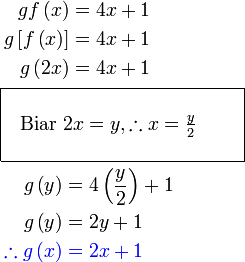
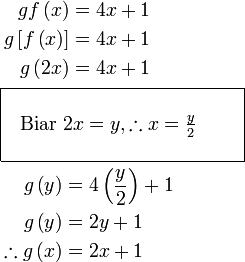 Semak :
Semak :
Semak :
Semak :
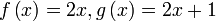 Semak :
Semak :
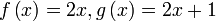
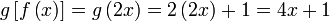
|
Nampak seperti yang sebelum ini, cuba dulu buat seperti tadi
Mula dengan fungsi gubahan, letak kurungan
Kita tumpukan pada
Bolehkah dibuat macam tadi?
Yang diberi adalah
iaitu fungsi dalam, bukan fungsi luar seperti tadi
Jadi sebenarnya lagi senang diganti
Apa yang boleh dibuat dengan 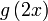 ?
Ganti ?
Ganti 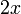 ke dalam ke dalam 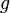 ?
Ganti ?
Ganti 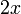 ke dalam ke dalam 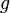 ? ?Tetapi kita tiada 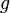 , dan , dan 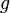 yang dicari sebenarnya
Kita hendak cari yang dicari sebenarnya
Kita hendak cari 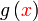 , tapi yang ada sekarang adalah , tapi yang ada sekarang adalah 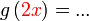 Kita hendak cari
Kita hendak cari 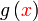 , tapi yang ada sekarang adalah , tapi yang ada sekarang adalah 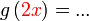 Bolehkah kita terus "pindah" 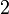 tersebut?
iaitu tersebut?
iaitu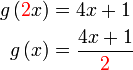 iaitu
iaitu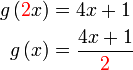 Sudah tentu tidak. Ingat bahawa 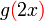 bukan bermaksud darab
Apakah maksud bukan bermaksud darab
Apakah maksud 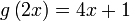 sebenarnya?
Apakah maksud sebenarnya?
Apakah maksud 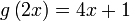 sebenarnya? sebenarnya?
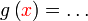 iaitu objek sepatutnya Apakah yang sebenarnya perlu dicari? 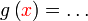 iaitu objek sepatutnya satu pembolehubah tunggal Masalahnya di sini kita tidak boleh tukar 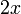 kepada kepada 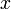 dengan begitu sahaja
Adakah semestinya objek ialah dengan begitu sahaja
Adakah semestinya objek ialah 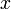 ?
Adakah semestinya objek ialah ?
Adakah semestinya objek ialah 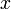 ? ?Tidak. Ingat bahawa 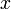 hanya mewakili objek. Kita boleh guna pembolehubah mana-mana
Misalnya hanya mewakili objek. Kita boleh guna pembolehubah mana-mana
Misalnya 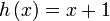 dan dan 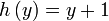 adalah sama
Misalnya adalah sama
Misalnya 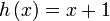 dan dan 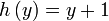 adalah sama adalah samaYang penting di sini objek sepatutnya Misalnya 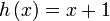 dan dan 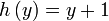 adalah sama adalah samaYang penting di sini objek sepatutnya suatu pembolehubah tunggal Jadi langkah seterusnya adalah menukarkan Jadi langkah seterusnya adalah menukarkan 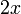 kepada
Jadi langkah seterusnya adalah menukarkan kepada
Jadi langkah seterusnya adalah menukarkan 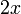 kepada satu pembolehubah yang tunggal, misalnya kepada satu pembolehubah yang tunggal, misalnya 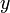 Paling baik buat di tepi atau dalam satu kotak supaya jelas
Kita buat begini supaya
iaitu objek sudah menjadi pembolehubah tunggal
Bagaimana dengan sebelah kanan?
Adakah begini?
Apakah masalahnya?
Paling baik buat di tepi atau dalam satu kotak supaya jelas
Kita buat begini supaya
iaitu objek sudah menjadi pembolehubah tunggal
Bagaimana dengan sebelah kanan?
Adakah begini?
Apakah masalahnya?
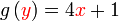
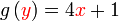 objek sudah 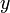 , di imej pun sepatutnya , di imej pun sepatutnya 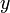 Jadi adakah
Jadi adakah 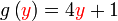 ?
Jadi adakah ?
Jadi adakah 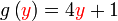 ? ?Tidak. Hubungan 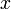 dengan dengan 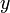 sudah kita takrifkan di dalam kotak. Kita sekarang perlu tukar sudah kita takrifkan di dalam kotak. Kita sekarang perlu tukar 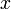 kepada sebutan dalam kepada sebutan dalam 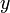 , jadi perlu susun dahulu.
Jadi gantikan
Ringkaskan
Adakah ini jawapan akhir?
Soalan minta , jadi perlu susun dahulu.
Jadi gantikan
Ringkaskan
Adakah ini jawapan akhir?
Soalan minta  , jadi perlu tukar balik kepada , jadi perlu tukar balik kepada 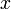 Adakah kita akan guna balik
Adakah kita akan guna balik 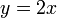 ?
Adakah kita akan guna balik ?
Adakah kita akan guna balik 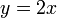 ? Tidak
Tujuan kita tukar ke ? Tidak
Tujuan kita tukar ke 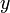 adalah supaya
Tujuan kita tukar ke adalah supaya
Tujuan kita tukar ke 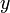 adalah supaya objek menjadi pembolehubah tunggal. Sememangnya sudah selesai dapatkan fungsi adalah supaya objek menjadi pembolehubah tunggal. Sememangnya sudah selesai dapatkan fungsi 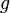 Hanya di sini kita perlu TULIS SEMULA dengan menggunakan
Hanya di sini kita perlu TULIS SEMULA dengan menggunakan 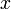 Seperti mana kita buat
Seperti mana kita buat
|
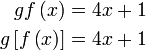
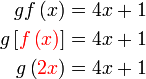
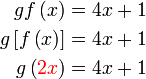
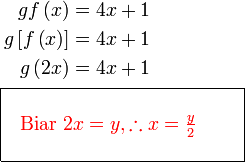
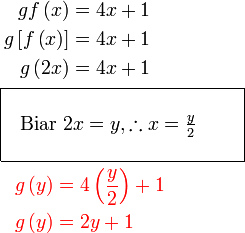
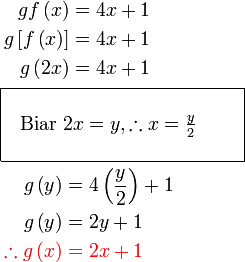
|
|
Sekali lagi Adalah penting untuk faham sebab setiap langkah Mula dengan fungsi gubahan dan letak kurungan Ganti apa yang boleh. Dalam kes ini, fungsi dalam diberi Masalah di sini ialah objek bukan satu pembolehubah tunggal Jadi tukarkan ke pembolehubah tunggal. Pada masa sama, 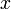 yang lain juga perlu ditukarkan, jadi susun dahulu
Tukarkan semua ke yang lain juga perlu ditukarkan, jadi susun dahulu
Tukarkan semua ke 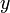 dan ringkaskan jika boleh
Tulis semula menggunakan dan ringkaskan jika boleh
Tulis semula menggunakan 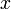 dan jangan lupa semak dan jangan lupa semak
|

Contoh 2
Diberi 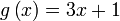 dan dan 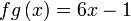 . Cari . Cari 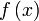
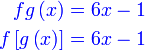
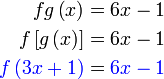
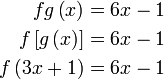 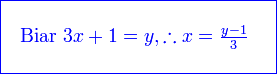
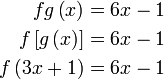 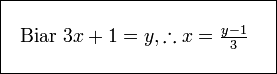 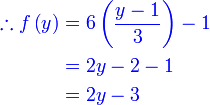
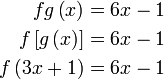 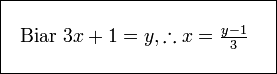 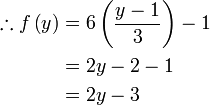 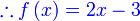 Semak :
Semak :
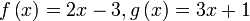 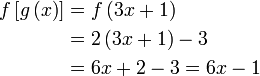
|
Cuba sendiri dahulu
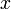 yang lain juga perlu ditukarkan, jadi susun dahulu
Tukarkan semua ke yang lain juga perlu ditukarkan, jadi susun dahulu
Tukarkan semua ke 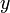 dan ringkaskan jika boleh
Tulis semula menggunakan dan ringkaskan jika boleh
Tulis semula menggunakan 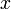
|
Bandingkan
Diberi 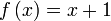 dan dan 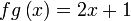 . Cari . Cari  . .
|
Diberi 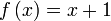 dan dan  . Cari . Cari  . .
|
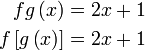
|
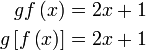
|
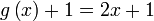
|
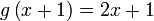
|
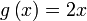
|
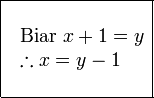 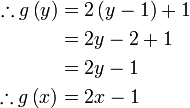
|
|
Semak
|
Semak
|
| Diberi | Jenis |
|---|---|
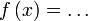 dan dan 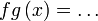
|
A
|
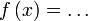 dan dan 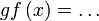
|
B
|
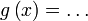 dan dan 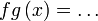
|
B
|
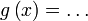 dan dan 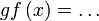
|
A
|